Publications
Highlights
For a full list of publications see Google Scholar
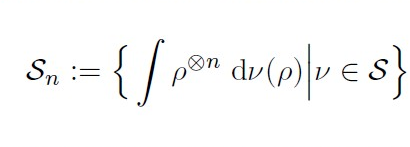
We extend quantum Stein’s lemma in asymmetric quantum hypothesis testing to composite null and alternative hypotheses. As our main result, we show that the asymptotic error exponent for testing convex combinations of quantum states against convex combinations of quantum states can be written as a regularized quantum relative entropy formula. We prove that in general such a regularization is needed but also discuss various settings where our formula as well as extensions thereof become single-letter.
M.Berta, F. G. S. L. Brandao, C. Hirche
Communications in Mathematical Physics 385, 55–77 (2021)
We introduce sequential analysis in quantum information processing, by focusing on the fundamental task of quantum hypothesis testing. Our goal is to discriminate between two arbitrary quantum states with a prescribed error threshold, ϵ, when copies of the states can be required on demand. We obtain ultimate lower bounds on the average number of copies needed to accomplish the task. We give a block-sampling strategy that allows to achieve the lower bound for some classes of states. The bound is optimal in both the symmetric as well as the asymmetric setting in the sense that it requires the least mean number of copies out of all other procedures.
E. Martínez-Vargas, C. Hirche, G. Sentís, M. Skotiniotis, M. Carrizo, R. Muñoz-Tapia, J. Calsamiglia
Physical Review Letters 126 (18), 180502 (2021)
First, we establish the strong Stein’s lemma for classical-quantum channels by showing that asymptotically the exponential error rate for classical-quantum channel discrimination is not improved by adaptive strategies. Second, we recover many other classes of channels for which adaptive strategies do not lead to an asymptotic advantage. Third, we give various converse bounds on the power of adaptive protocols for general asymptotic quantum channel discrimination.
M. M. Wilde, M. Berta, C. Hirche, E. Kaur
Letters in Mathematical Physics 100, 2277-2336 (2020)
In classical information theory, the information bottleneck method (IBM) can be regarded as a method of lossy data compression which focusses on preserving meaningful (or relevant) information. As such it has recently gained a lot of attention, primarily for its applications in machine learning and neural networks. We prove the convexity of the quantum IB function, and then giving an alternative operational interpretation of it as the optimal rate of a bona fide information-theoretic task,
N. Datta, C. Hirche, A. Winter
Proc. ISIT 2019, 7-12 July 2019, Paris, pp. 1157-1161
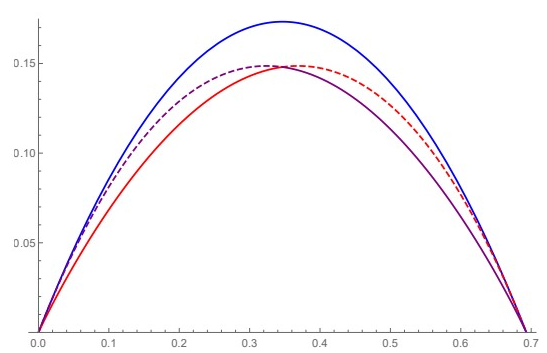
Bounds on information combining are entropic inequalities that determine how the information (entropy) of a set of random variables can change when these are combined in certain prescribed ways. Such bounds play an important role in classical information theory, particularly in coding and Shannon theory; entropy power inequalities are special instances of them. The arguably most elementary kind of information combining is the addition of two binary random variables (a CNOT gate), and the resulting quantities play an important role in Belief propagation and Polar coding. We investigate this problem in the setting where quantum side information is available.
D. Reeb, C. Hirche
IEEE Trans. Inf. Theory 64, 4739-4757 (2018)
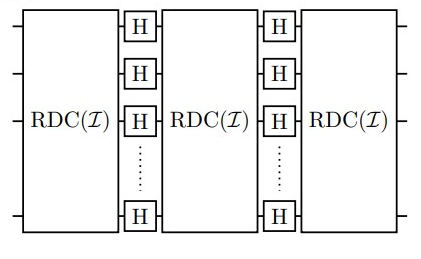
We provide new constructions of unitary t-designs for general t on one qudit and N qubits, and propose a design Hamiltonian, a random Hamiltonian of which dynamics always forms a unitary design after a threshold time, as a basic framework to investigate randomising time evolution in quantum many-body systems. The new constructions are based on recently proposed schemes of repeating random unitaires diagonal in mutually unbiased bases.
Y. Nakata, C. Hirche, M. Koashi, A. Winter
